向量代数与空间解析几何

空间向量

方向角

$$
\alpha=\frac{a_x}{|a|}=\frac{a_x}{\sqrt{a_x^2+a_y^2+a_z^2}}
$$

$$
\beta=\frac{a_y}{|a|}=\frac{a_y}{\sqrt{a_x^2+a_y^2+a_z^2}}
$$

$$
\gamma=\frac{a_z}{|a|}=\frac{a_z}{\sqrt{a_x^2+a_y^2+a_z^2}}
$$

四点共面

混合积

$$
[abc]=(a\times b)\cdot c
$$

三向量共面

$$
[abc] = 0
$$

斜四棱柱体积

$$
V=[abc]
$$

空间平面

点法式方程

$$
过一点M_0(x_0,y_0,z_0)且以\vec n={A,B,C}为法向量的平面\pi的方程
$$

$$
A(x-x_0)+B(y-y_0)+C(z-z_0)=0
$$

一般方程

$$
记D=-(Ax_0+By_0+Cz_0)
$$

$$
A(x-x_0)+B(y-y_0)+C(z-z_0)+D=0
$$

截距式方程

$$
记a=-\frac{D}{A},b=-\frac{D}{B},c=-\frac{D}{C},
$$

$$
\frac{x}{a}+\frac{x}{b}+\frac{x}{c}=0
$$

二面角

$$
\cos\theta=\frac{|n_1\cdot n_2|}{|n_1||n_2|}=\frac{|A_1A_2+B_1B_2+C_1C_2|}{\sqrt{A_1^2+B_1^2+C_1^2}\sqrt{A_2^2+B_2^2+C_2^2}}
$$

点到直线的距离

$$
d=\frac{|n\cdot\overrightarrow{M_0M_1}|}{|n|}=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}
$$

平面束方程

$$
\lambda(A_1x+B_1y+C_1z+D_2)+\mu(A_2x+B_2y+C_2z+D_2)=0
$$

空间直线

一般方程

点方向式方程&对称式方程

$$
过M_0(x_0,y_0,z_0)且方向向量为s={m,n,p}的直线
$$

$$
\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}
$$

参数方程

线线角

$$
\cos\varphi=\frac{|s_1\cdot s_2|}{|s_1||s_2|}=\frac{|m_1m_2+n_1n_2+p_1p_2|}{\sqrt{m_1^2+n_1^2+p_1^2}\sqrt{m_2^2+n_2^2+p_2^2}}
$$

线面角

$$
\sin\varphi=\frac{|s\cdot n|}{|s||n|}=\frac{|Am+Bn+Cp|}{\sqrt{m^2+n^2+p^2}\sqrt{A^2+B^2+C^2}}
$$

空间曲面

柱面

旋转曲面

$$
例如以z轴为轴，f(y,z)=0为母线的旋转曲面
$$

$$
令y=\pm\sqrt{x^2+y^2}
$$

$$
曲面方程：f(\pm\sqrt{x^2+y^2},z)=0
$$

二次曲面

椭球面

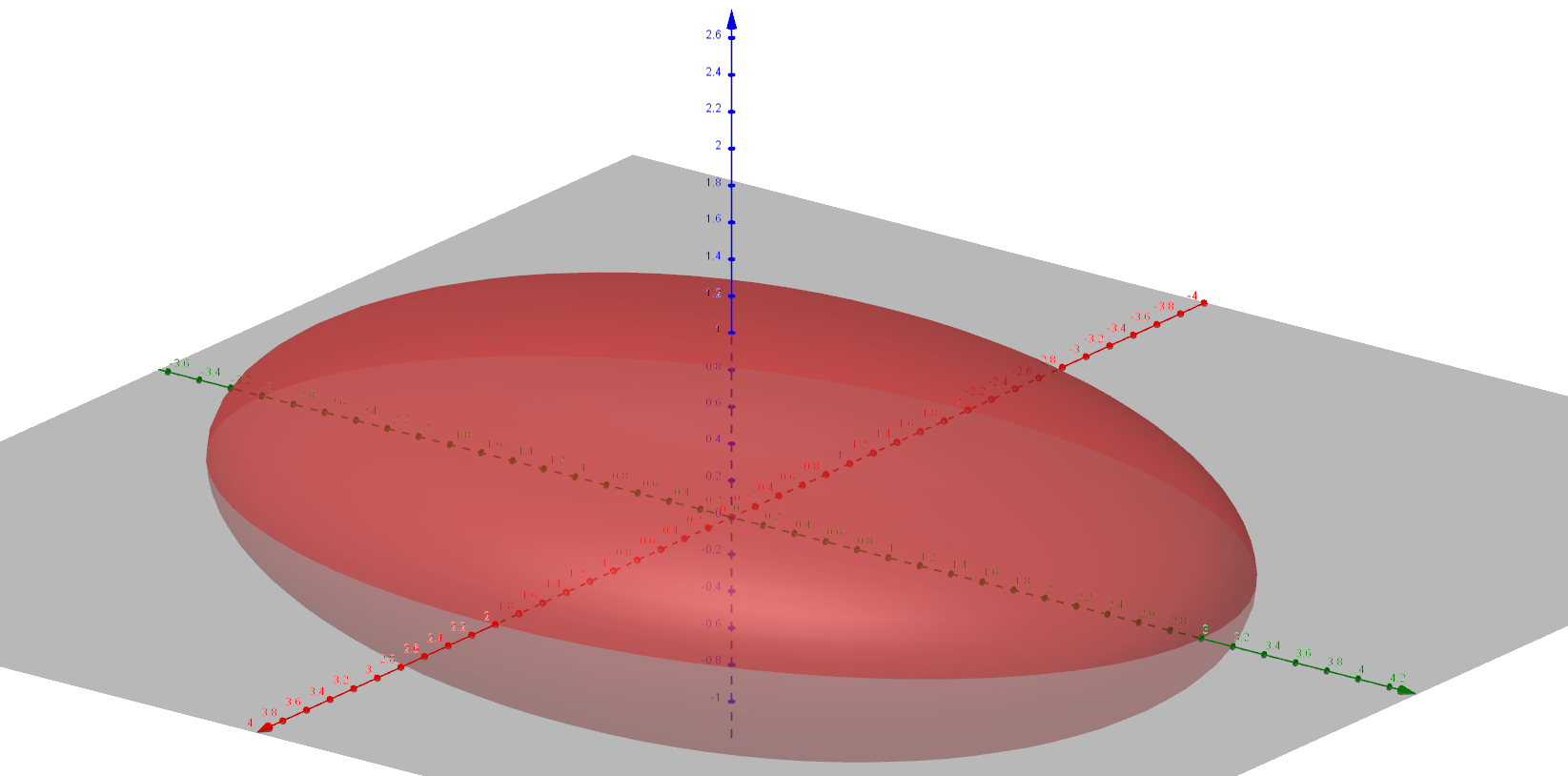$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{y^2}{c^2}=1，(a>0,b>0,c>0) $$

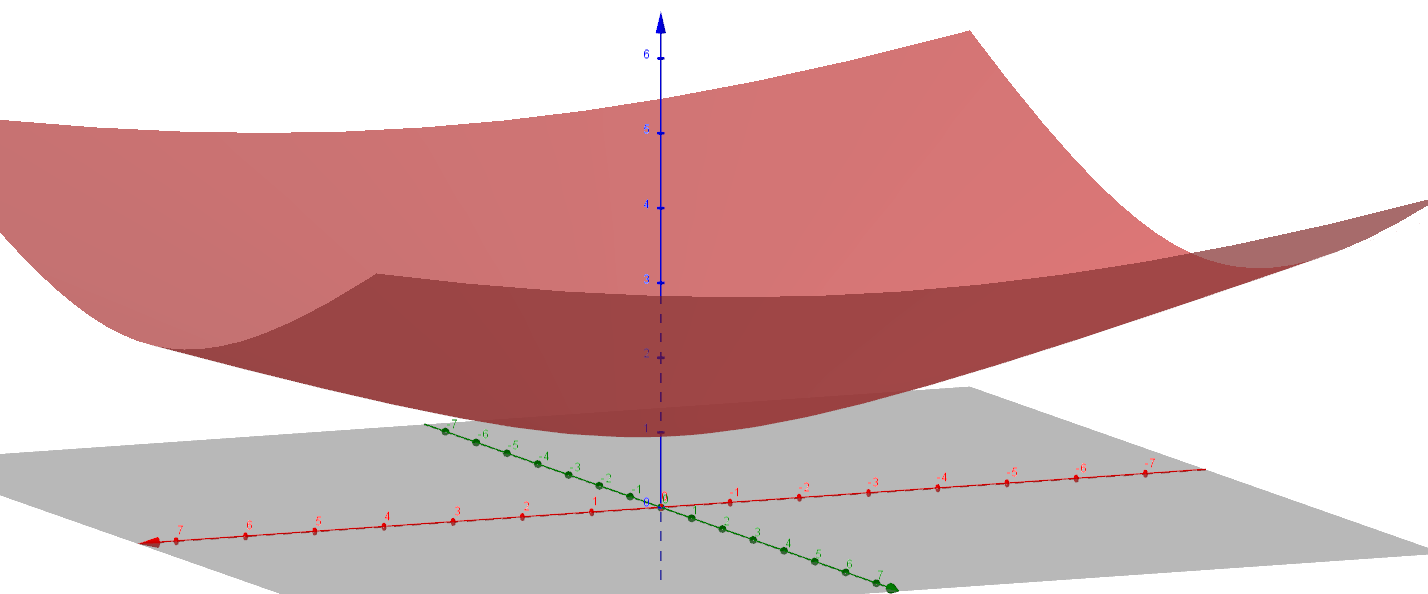
椭圆抛物面

$$ \frac{x^2}{2p}+\frac{y^2}{2q}=z，(p,q同号) $$

双曲抛物面

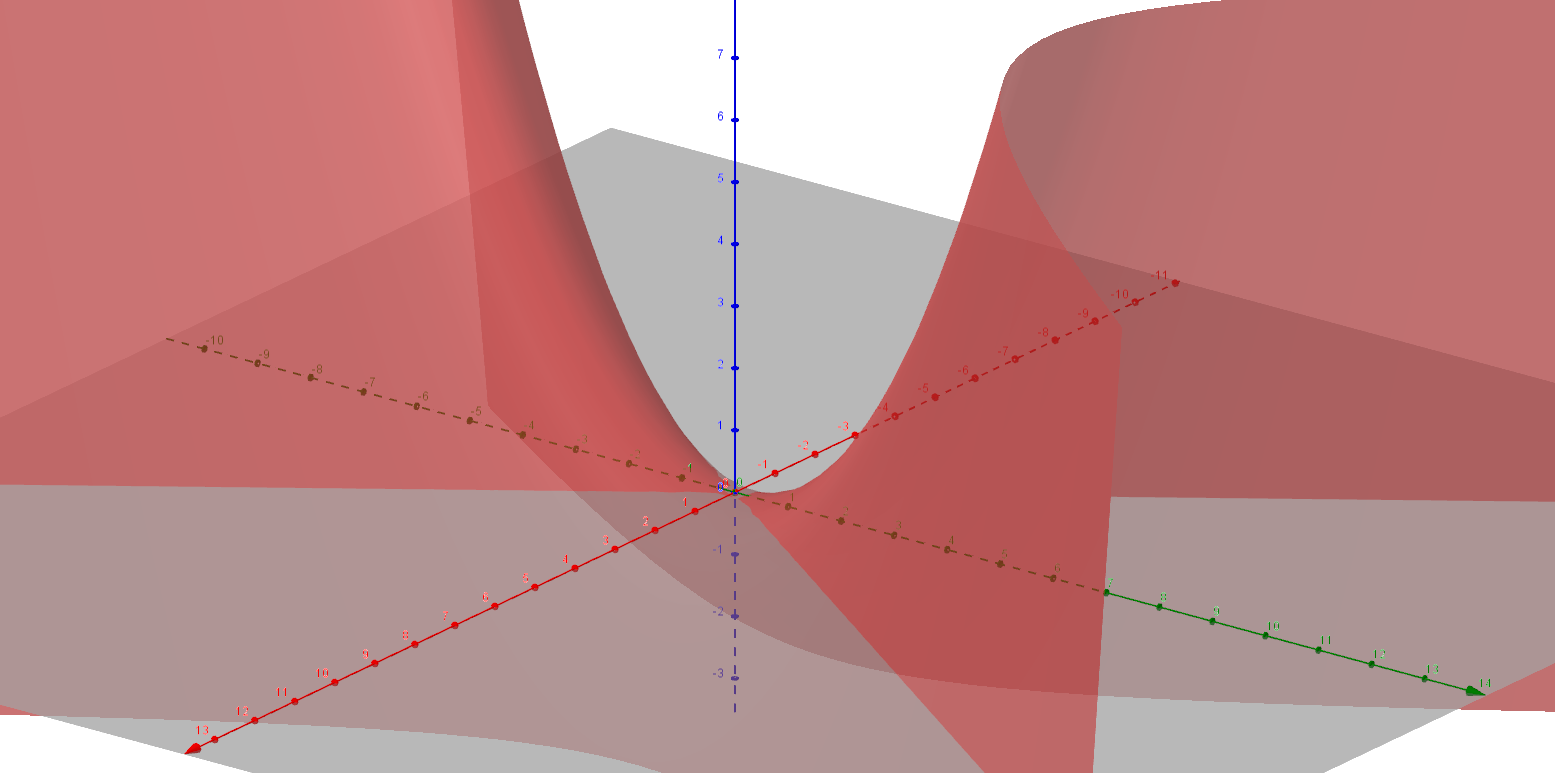$$ -\frac{x^2}{2p}+\frac{y^2}{2q}=z，(p,q同号) $$

单叶双曲线

$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{y^2}{c^2}=1，(a>0,b>0,c>0) $$

双叶双曲线

$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{y^2}{c^2}=-1，(a>0,b>0,c>0) $$